Historical

Surely, Newton's Theory of Gravitation (1687) is one of the most important theories in the history of science. It is not only able to describe the falling of an apple, but also the formation of a galaxy. The equation of gravitational force is one of the greatest conquests of Mankind:

When Newton published “Opticks” in 1704, he belived in the corpuscular nature of ligth, and he ensured that it must exist a relation between ligth and matter, with the form of a gravitational force ruled by equation [1].

In 1804 (two centuries ago), Soldner was the first who calculated that, for small angles, the Newtonian deflection of light by a massive object should be [SOL04]:

where M is the mass of the deflecting object and R is the deflection impact parameter. For a light ray grazing the Sun this gives a deflection angle

(a scheme is shown in figure 1). This work was considered a theoretical curiosity and could not be tested observationally, because of the lack of precision of telescopes in 1804.

figure 1: Newtonian angle of deflection of light by the Sun.

Although Newton’s Theory of Gravitation was acepted by scientists along centuries, it was not able to explain several anomalies, the most famous of these being the perihelion shift of Mercury. Classical mechanics could explain the majority of the observed shift, but a residual shift of

per century could not be explained by the gravitational effects of other planets.

During the earlier part of this century, Einstein extended his Special Theory of Relativity to generalized, or accelerating reference frames [EIN15]. From this study emerged a new description of gravity which saw gravitational force as the curvature of a space-time, the curvature being due to the presence of mass. General Relativity, as this theory is known, not only explained the residual shift in Mercury's perihelion, but also predicted other effects, including the bending of light in a gravitational field. General Relativity predicts that the bending angle for a light ray in the vicinity of a point mass to be [WEI72]:

precisely double the value expected from Newtonian gravity (see equation [2]). With this, light rays grazing the surface of the Sun are bent by an angle of

(see figure 2). This value is not twice that obtained by Soldner due to differing estimates for the solar mass and radius at the time of calculation.

figure 2: Einstein’s angle of deflection of light by the Sun. Eddington’s experiment.

In 1919, Eddington (on Principe Island) and Crommlin (in Brazil), monitored the position of the stelar background during the solar eclipse of the

May, and they obtained a value for the deflecting angle of light by the sun of

and

respectively, with quoted errors of

. These results confirmed the Einstein’s prediction [EDI19].

In the following decades, light deflection or Gravitational Lensing (GL) was only very rarely the topic of a research paper: In 1924, Chwolson [CHW24] mentioned the idea of a “fictitous double star” and the mirror-reversed nature of the secondary image. He also mentioned the symmetric case of star exactly behind star, resulting in a circular image. Einstein also reported in 1936 about the appearance of a “luminous circle” (“Einstein Ring”, see figure 3) for perfect alignment between source and lens [EIN36], and of two magnified images for slightly displaced positions. Influenced by Einstein, Fritz Zwicky [ZWI37] pointed out in 1937 that galaxies (“extragalactic nebulae”) are much more likely to be gravitationally lensed than stars and that one can use the gravitational lens effect as a “natural telescope”.

figure 3: Concept of “Einstein Ring”.

In the 1960’s, a few partly independent theoretical studies showed the usefulness of lensing for astronomy. In particular, Sjur Refsdal derived the basic equations of Gravitational Lens Theory and subsequently showed how the gravitational lens effect can be used to determine Hubble's Constant by measuring the time delay between two lensed images [REF64], [REF66].

When quasars were discovered in the 1960’s, Barnothy [BAR65] was the first to connect them with the gravitational lens effect.

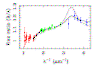
In 1979 the whole field received a real boost when the first double quasar (QSO 0957+561, see figure 4) was discovered and confirmed to be a real gravitational lens by Walsh, Carswell & Weymann [WAL79].

figure 4: Components of double quasar QSO 0957+561.