Old Q0957+561 data & software:
► Simple FORTRAN programs to apply the d2 test (accurate and robust time delay measurements)
► Photos
Advertising:
Introduction to GL
(iii)
Magnification & Critical curves
Ligth deflection in a graviational
field not only changes the direction of a ligth ray, but also the cross-section
of a bundle of rays. Since gravitational ligth deflection is not connected
with emission and absortion, the specific intensity Iu is constant along the ray. The flux
of ane image of an infinitesimal source is the product of its surface brigthness
and the solid angle Dw it
subtends on the sky. Then the ratio of the flux of a sufficiently small image
to that of its corresponding source in absence of the lens, is given by the
“magnification factor” [SCH92]:
[22]
If we consider an infinitesimal
source at
that subtends a solid angle Dwsource , and an image with solid angle Dwimage at a position
; then the relation of the two solid angles is determined by the area distortion
of the lens mapping equation [17], and given by (from definition of solid angle):
[23]
It is evident that the
area distortion caused by the deflection is given by the determinant of the
jacobian matrix of the lens mapping
. From [22] we find:
[24]
If a source is mapped into
several images, the ratios of the respective magnification factors are equal
to the flux ratios of the images.
The magnification factor is
always positive, because of its definition. The determinant of the jacobian
matrix of the lens mapping can be negative, however. When that determinant
is negative for an image, it is said that image possess “negative parity”,
i.e. it is inverted.
It is easy to study the magnification
factor for a Schwarzschild lens, because of the simple geometry of the problem.
If we introduce in equatios [9a], [9b]
the normalized angles:
[25]
we obtain:
[26]
With normaliced solid
angle
for the source and normaliced solid angle
for the images. Then,
according to [24]:
[27]
From [26], after a little algebra:
[28]
where, for
, the subindex a implies positive parity and b implies negative
parity. It is interest to note that the magnification factor diverges if
(condition for the Einstein ring, as shown before),
so we note:
, which means that the Einstein Ring is a critical curve for the Schwarzschild
lens.
While
and
are quite similar for
, the two images are of quite different brigthness if
is not near 0. The flux ratio:
[29]
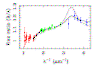
is shown in figure 7.
|
|
|
figure 7: The angular separation of the two
images produced by a Schwarzschild lens, in units of qE (red line), the
magnification ma of the primary image (green line), the magnification mb of the secondary image (dark blue line),and the absolute value of the
ratio ma/mb (ligth blue
line). |
The previous calculations are rigth for a Schwarzschild Lens
and puntual sources, but they are not valid for explain the lensing event
when the source is a extended one. For a puntual source, is evident
from [28] that:
[30]
If we integrate [30] over the entire source, we will obtain the total
magnification for an extended source:
[31]
where we have considered
the special case of a uniform circular source and an angular radius
, exactly behind the lens.
Click on the arrow below to return to the previous page.
